
If you are young or just graduated from college, the last thing on you mind might be saving for retirement. After all, you still have plenty of time right, since retirement is still over 40 years away. Wrong. The best time to start saving for retirement is right now.
Yes, you could start saving in five or ten years and live it up in your twenties traveling and going out every weekend, but it will cost you. It will cost you a lot more than you think because of a phenomenon called compound interest.
Think of compound interest as being a snowball at the top of a mountain and a snowflake as a dollar. A snowflake might not seem like much, but once those snowflakes start adding up, it becomes a snowball that starts rolling down the mountain. On its way down the mountain, the snowball picks up more snow and it gets bigger and soon becomes unstoppable. By the time it gets to the bottom of the mountain, that snowball is the size of a building. The earlier you start saving, the higher up the mountain you start and the bigger the snowball at the bottom.
Table of Contents
What Is Compound Interest?
When people think of interest, they usually think of debt. Things like car loans, credit card balances, title loans, and personal loans are the bad kind of interest because it makes things cost more.
Compound interest can be thought of as interest earned from the initial principal plus the interest accumulated from earlier periods. Compound interest from savings and investments is the good type of interest you’d want because it’s your money making more money for you.
During the initial periods of saving, it will appear that money and one’s net worth is growing extremely slowly, which can be discouraging for a beginner. Once your money stash gets bigger, the power of compound interest will make your wealth grow exponentially.
Have you heard people mention that making their first million was the hardest? Some of those who have hit the two comma club have found that their second million arrived a lot quicker, and a big part of that is from compound interest. It might seem like a million is really far off when one is starting from zero, but the earlier you start saving, the quicker you’ll get there.
Compound Growth of a $5,500 Contribution
Using our Compound Interest Calculator, if a 22 year old makes a single $5,500 contribution to a Roth IRA account at their first job upon graduating from college while earning a 8% annual return, and doesn’t touch that money until retirement at 67 years old, that $5,500 investment will grow to $198,900 after 45 years.
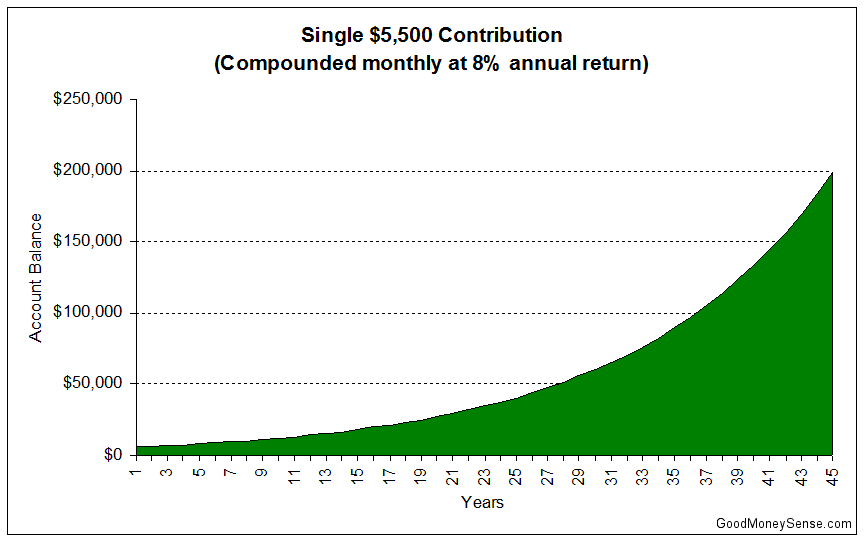
As you can see from the above chart, at first the account balance grows at a slower rate in the first few decades. Then as the balance gets bigger, the earnings start increasing exponentially, and by the 45th year the account earns over fifteen thousand dollars a year or three times the initial deposit.
Start Saving Now or Save A Lot More Later
The formula to calculate compound interest is A = P(1+ r/n)nt
Note that the P is the principal, r is the interest rate, n is the number of times interest is compounded per year, and t is number of years saved or invested. The starting principal and the interest rate has an effect on the ending amount, but time is the important component of the compound interest formula. The principal is only a multiplier in the formula while the time is an exponent; the greater the time, the greater the amount.
Lets consider three friends Peter, Paul, and Mary. They all receive the same 8% annual return on their investments. The only difference is how early they started saving.
- Peter starts investing at 25 years old, saving $5,000 a year for 10 years until he turns 35 and then stops contributing after saving $50,000 total.
- Paul starts investing at 35 years old, saving $5,000 a year until he retires 30 years later at 65 years old. He has saved a total of $150,000.
- Mary is a dedicated saver who starts saving $5,000 a year at 25 years old for 40 years until she retires at 65. She has saved a total of $200,000 in her retirement account.
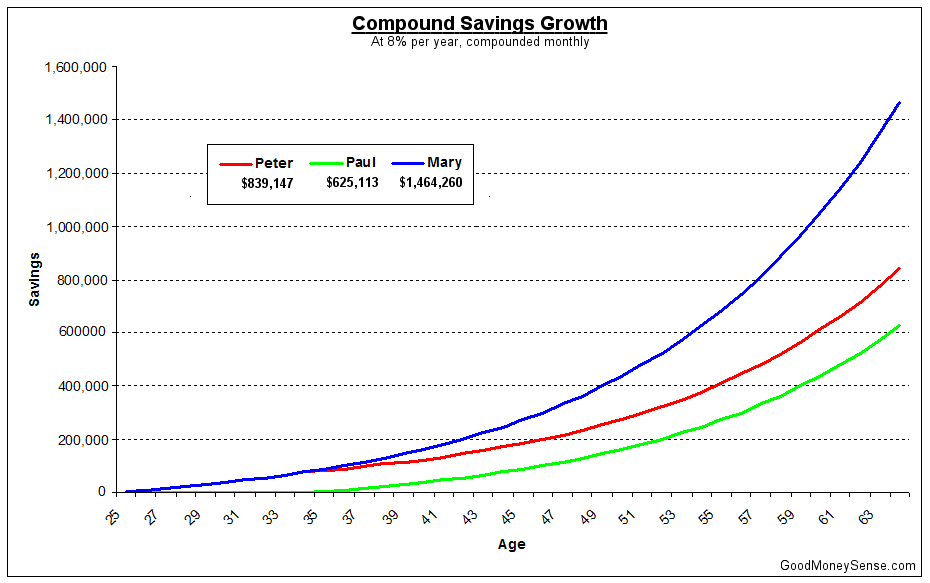
Between Peter and Paul, who has more money at 65? If you guessed Peter, you are absolutely correct. Even though Paul has deposited three times more money than Peter, he still doesn’t catch up to Peter’s total. In fact, Paul could continue depositing $5,000 every year for two lifetimes and he will still never catch up.
Now consider Mary’s situation. She both started early and never stopped contributing to her account. She has become a millionaire by steadily saving only $416 a month.
If Paul had wanted to catch up to Mary’s amount by the age of 65, he would have had to save almost $950 a month because he started 10 years later. Which is easier to save? $416 a month or $950 a month?
The Rule of 72
The Rule of 72 says that if you divide 72 by the annual return rate, you will get the number of years it will take to double your money. In our example above, we used 8% for the interest rate, so 72/8 = 9 years. Every 9 years, the size of the account will be doubled from the previous 9 years if you do not touch the money.
The interesting thing about this is the 8% interest rate I am using in this example is hypothetical. If you invested your retirement account in the S&P 500 index fund, your average annualized return could be as high as 10% since the average total annual return for the S&P 500 for the past 90 years is 9.8% as of 2016. That means you could double your money every 7 years.
While past performance does not mean the S&P 500 index will get these rates in the future, those 90 years did include the Great Depression, the Great Recession, and many other smaller recessions in between. This brings us to another important point…
Invest For The Long Term
Once you put your money into a retirement account such as a 401k, don’t touch that money!
As tempting as it is to withdraw a 401k when you change jobs, investing for the long term will always beat short-term investing for the average investor. It is very hard to time the market but it is really easy to panic and try to cut your losses when seeing your balance in a free fall. Just ask those who sold in 2008 at the bottom of the recession only to miss the 23% run-up in 2009.
If you continue to contribute and invest during a downturn, you will be buying shares at a discount. This means you will be able to purchase more shares at a lower price, lowering the average total cost of your investments. This is called dollar cost averaging.
Once your money is invested, not taking that money back out for a year is good. Five years is better. Thirty years is best. Remember how the compound interest formula works and how time affects the total.
Another reason to stay for the long haul is frequent trading incurs trading fees and taxes, which will reduce your overall returns.
Get Started Now
If you are early in your career, it might seem like it is almost impossible to save any money. You might have student loans to pay off. You might have a car loan because you needed a way to get to your first job. You might have just graduated from college and moved out of your parents’ house and into your own apartment for the first time and had to buy all new furnishings, along with coming up with the first month’s rent and a security deposit.
Read More: Money Mistakes To Avoid Making In Your 20s
Or maybe you are older and are saving up for a house, kids’ college tuition, or a wedding. Either way, it’s hard to think about saving for retirement that is decades away when you have bills you need to pay today.
It is better to save something, anything, than nothing at all. One trick you’ve probably heard of is to pay yourself first. What this means is take the money you want saved out of your paycheck before it even hits your checking account and put it into another account. This way you won’t be tempted to spend it. Out of sight, out of mind. Start with a small contribution, even if it’s $20-$100 per month, and slowly increase it as you get used to not having that money available.
Read more: How To Save Money Without Even Trying
